タグ

, , , , , , , , , , , , , ,

こんにちは。今日は

どうして超光速のニュートリノを使えば、過去にメッセージが送れるのか

をお話ししたいと思います。過去にメッセージが送れるとなにが起こるかというと、「因果律」が破れます。

因果律が破れるって？

「因果律」というのは、原因と結果のこと。原因があるから結果があるということです。

例えば、こんなシチュエーションを考えてみましょう。地球にニュー君という男の子がいるとします。ニュー君はリノちゃんという女の子が好きです。

ニュー君は仕事帰りに、リノちゃんに電話して夕食にさそいます。↓

リノちゃんはあんまりニュー君に興味がありません。「いま、地球外なの」といって断ります。よくあることですね。

ここで、ニュー君は、リノちゃんが「イヤ」といって断ることを知っていれば、決して誘ったりしないのです。

もし、リノちゃんの「いま、地球外だからいけないわ」が先に届いていたとしたらどうでしょう。ちょっとおくびょうもののニュー君は「べつに訊いてないよ」といって知らないふりをします。

実はこれが、光速を超えて飛ぶ粒子が存在して、アインシュタインの相対性理論が正しいとすれば考えうるのです。

リノちゃんが本当に地球外にいて、ロケットでかなりのスピードで遠ざかっているとします。そして超光速ニュートリノを使って通信します。

そうすると、ニュー君が「夕食どう？」と訊く前に「いま、地球外なの」が先に届いてしまうのです。

どうしてこうなるのかを、ご説明しましょう。

アインシュタインの時間と空間

宇宙のなかは、いろいろな出来事で満たされています。この出来事を「イベント」と呼びましょう。宇宙の誕生も銀河の生成も星の爆発も、リノちゃんの「いま、地球外なの」発言も、全部イベントです。

個々のイベントは因果律を保っていなくてはなりません。

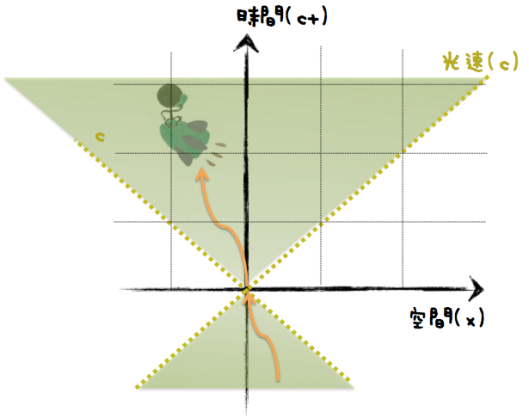
アインシュタインは、これらのイベントを時間と空間のうえに描きました。アインシュタインにとっての時間と空間はこんな感じ。↓

x軸が空間で、y軸が時間です。直角に交わっています。ゼロが現在、現地点を表しています。

ちょうど45度のところでひかれている点線は、光速で移動した場合の線。

世の中、光速以上で移動できるものはないはずなので、この45度の線を超えることはできません。

つまり、ゼロ地点にいる人に起こりうる全てのイベントは、この45度の線内である必要があります。それが薄緑で表されている領域です。この領域を光円錐と呼びます。

さて、この時空の図は、実は止まっている（静止している）人にとっての図です。例えば地球上の人としましょう。（本当は地球はかなりの速さで宇宙空間を滑走していますが）

地球外にいて、地球近辺をかなりの速さで通過しているリノちゃんの時空の図は、ちょっと違ってきます。

でも光の速度は、誰にとっても同じはず。

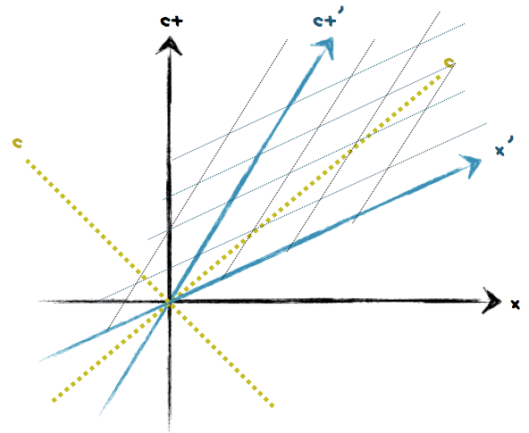
動いているリノちゃんの時空の図を重ね合わせると、こんな感じになります。↓　青い時空軸に注目。

x’軸がリノちゃんにとっての空間、y’軸が時間。

光の速度は変化していませんね！

さて、リノちゃんの時空はもはや直行していません。同時刻の線と同位置の線を何本か付け加えると、こうなります。

地球の軸と違って、ななめってます。

因果律が破れるわけ

さて、では本題に戻りましょう。

地球上にいるニュー君と、地球から遠ざかっているリノちゃんが、ある二つのイベントを見ているとしましょう。イベント「相（あい）」とイベント「対（たい）」です。

そして、「相」が起こると、「対」まで超光速のニュートリノで伝えられるとしましょう。

そうすると、光円錐を超えることができるということですので、「相対」の関係をニュー君とリノちゃんの時空に描くと、こうなります。（緑の矢印）

ここで、二人の時間軸に注目してみましょう。

直行しているニュー君の時空では、「相」が過去で「対」が未来になっています。つまり、「相」が起こってから「対」が起こっているということです。

ところが！ななめっているリノちゃんの時空では、「相」の前に「対」が起こっているではありませんか！

 ニュー君にとって「相対」がリノちゃんにとっては「対相」になるのです。

これが、因果律が破れてしまうという、シンプルな説明です。

さらに、メッセージを受け取ったリノちゃんが超光速で送り返すと、こんな感じでしょうか。（紅い矢印）

（ちょっと強引ですが）ニュー君は、メッセージを送る前に受け取ることになります。

異次元へのいざない

こんなことがあっていいのでしょうか。いいはずがありません。

アインシュタインはこの問題を、光速を超える粒子は存在しない、として封印したのです。

しかし、相対論という理論としては、光速を超える粒子を否定していません。ずっと光速を超えたままで、45度の線さえ超えなければ問題はないのです。

ですので、相対論に基づく理論であっても、光速を超える粒子を予言していたり、矛盾なく説明できるものがあります。

そこで理論家さんたちが、こぞって超光速粒子を説明する理論を出しています。なかには奇妙な「場」で宇宙を満たすことによって、ニュートリノが光速を超えたり超えなかったりする現象を説明するものも。

ここでは異次元の理論をみてみましょう。

例えば、超ひも理論とよばれる理論。これは、全ては小さくしていくと、「ひも」でできている、とする理論です。

考えてみると、物質をずっと小さくしていくと、別に1次元の「点」にたどりつかなくてはいけない理由はないのです。2次元の広がりをもった「線」、つまり「ひも」であってもよいわけです。

この超ひも理論では、空間は3次元ではなく少なくとも9次元になっています。超ひも理論にもいろいろあるのですが、超光速の粒子が導きだされるものもあります。

超ひも理論でなくても、異次元を用いれば超光速ニュートリノを説明できる、という人たちもいます。

3次元以上の空間が存在していて、私たちは3次元のシートに閉じ込められているとします。ニュートリノは異次元を旅し、また戻ってきます。バケツにはった水が跳ねて、また水面に戻ってくる感じだといいます。戻ってくるときには、過去の水面には戻らないので、因果律は破れないのです。

こんなふうな異次元理論はいっぱい存在します。

私たちの住む時空は歪曲しているとしましょう。そして、ニュートリノはステライル・ニュートリノという、別種のニュートリノ（まだ仮想）に変身するかもしれません。これは時空のショートカットをとることができるので、また普通のニュートリノに戻ったときには速くなっているように見えます。

異次元があるといろんな可能性が広がります。

でも個人的に・・・これはあんまり美しい理論ではないのでは、と思ってしまいます。

異次元があるとけっこういろいろ解決できてしまう

異次元の理論はけっこう歴史があります。

相対論についてみてみましょう。相対論には二種類あります。1905年に発表された「特殊」相対性理論と、1915年の「一般」相対性理論です。

上で図を使って説明した相対論は、「特殊相対性理論」で、ある二つの現象を統合した美しい理論です。

ここで統合したのは「静止しているということ」と「動いているということ」という二つの現象。宇宙のある一点でとどまっている人と、あるスピードを持って動いている人とでは、周りのものがどう見えるのかを深く掘り下げて考えたのです。

この二つの統合は、すでにニュートンによってなされていたのですが、アインシュタインはこれに「誰にとっても光の速度は一定」の説明を付け加えてアップグレードさせました。

つまり、光の理論である「電磁場の理論」も一緒に統合したのです。このとき、ついでに時間と空間までも統合してしまいました。

相対性理論はこのようにたくさんの物理現象を一度に統合できるので、「美しい理論」といわれています。

次に、アインシュタインは電磁場の理論と重力の理論を統合します。これが「一般相対性理論」。

しかし、アインシュタインがこれを提唱するまえに、実はフィンランドのノードストームという人が、電磁場の理論と重力の理論を統合しています。

ノードストームはここで異次元を導入したのです。3次元の空間を4次元にするだけで、いとも簡単に二つの理論を完全に統合させてしまえるのです！

しかしこれは、直後のアインシュタインの一般相対性理論によって一蹴されました。

アインシュタインは、「重力の理論」と「相対性」を統合することによって、電磁力の理論のみならず、「静止していること」、「動いていること」、「速度を変えながら動いていること」など、さまざまな「動き」をも統合しました。

そしてこの一般相対性理論は、今では、最も実証された理論となっています。

一方で、次元を加えればいろいろ説明できてしまう。他方で、もっと美しい理論があるはず、と考えてしまう。これが、異次元に慎重になってしまう理由です。